Введение в ТАУ
Прежде всего, если речь идет об управлении, то имеется объект управления, т.е. некий механизм, агрегат или устройство, некий технологический, энергетический или транспортный процесс, желаемое поведение или протекание которого должно быть обеспечено. Поведение объекта управления, результат его действия определяется некоторыми показателями. Чаще всего ими являются значения каких-то физических величин, которые называют выходными величинами или координатами объекта управления.
 |
Предмет дисциплины и историческая справка |
|
В реальных условиях на каждое устройство или процесс многочисленные воздействия оказывает внешняя среда. Все воздействия, с точки зрения их влияния на действие объекта, на его выходные величины, разделяются на две принципиально отличительные группы. Некоторые из воздействий обеспечивают желаемое изменение поведения объекта, достижение поставленных целей. Такие воздействия называют управляющими, при их отсутствии задача управления вообще не имеет решения.
Другие воздействия, напротив, мешают достижению цели, и изменить их, как правило, невозможно. Такие воздействия называют возмущающими (или просто возмущениями).
Задача управления, по существу, заключается в формировании такого закона изменения управляющих воздействий, при котором достигается желаемое поведение объекта независимо от наличия возмущений.
Сложная и разностороння задача управления включает более узкую задачу регулирования, которую главным образом и будем рассматривать в дальнейшем. Задача регулирования заключается в поддержании выходных величин объекта равными (или пропорциональными) некоторым эталонным функциям времени - задающим воздействиям. Последние могут быть постоянными или изменяющимися как по заданному, так и по заранее неизвестному закону.
Объект управления может принадлежать как к неживой природе, в частности, быть техническим устройством, так и к живой природе (коллектив людей). В свою очередь, само управление также может осуществляться как человеком (пилот управляет самолетом), так и техническим устройством (самолетом управляет автопилот).
Управление, осуществляемое без участия человека, называется автоматическим управлением. Предметом настоящей дисциплины является теория автоматического управления техническими объектами. Общая теория управления, охватывающая как неживую, так и живую природу, является предметом науки кибернетики. Теория автоматического управления - часть кибернетики.
Для осуществления автоматического управления создается система, состоящая из объекта управления и управляющего устройства, или регулятора. Такая система соответственно называется системой автоматического управления.
Впервые, по-видимому, с необходимостью построения регуляторов столкнулись создатели высокоточных механизмов, в первую очередь - часов. Даже небольшие, но все время действующие в них помехи приводили в конечном итоге к отклонениям от нормального хода, недопустимым по условиям точности. Противодействовать этим помехам (возмущениям) чисто конструктивными средствами, например, улучшая обработку деталей, повышая их массу или увеличивая развиваемые устройствами полезные усилия, не удавалось, и для решения проблемы
точности в состав системы стали вводить регуляторы. На рубеже нашей эры арабы снабдили поплавковым регулятором уровня водяные часы. Гюйгенс в 1657 г. встроил в часы маятниковый регулятор хода.
Хотя отдельные автоматические регуляторы и появились в те далекие времена, они оставались любопытными для истории техники эпизодами и сколько-нибудь серьезного влияния на формирование техники и теории автоматического регулирования не оказали. Развитие промышленных регуляторов началось на рубеже XVIII и XIX столетий, в эпоху промышленного переворота в Европе. Первыми промышленными регуляторами являются автоматический поплавковый регулятор питания котла паровой машины, построенный в 1765 г. И.И. Ползуновым,
и центробежный регулятор скорости паровой машины, на который в 1784 г. получил патент Дж. Уатт. Эти регуляторы как бы открыли путь потоку предложений по принципам регулирования и изобретений регуляторов, относящимся к механике.
Первые публикации исследований в этой области начинаются с 30-х годов прошлого века (первая известная публикация Д.С. Чижова была в 1823 г.). Наиболее важными, признанными фундаментальными, явились три теоретические работы, содержащие основы новой науки. Это работы Д.К. Максвелла "О регуляторах" (1866) и работы И.А. Вышнеградского "Об общей теории регуляторов" (1876) и "О регуляторах прямого действия" (1877). Д.К. Максвелл и И.А. Вышнеградский рассмотрели машину (т.е. объект)
и регулятор как единую динамическую систему, обосновали общий методологический подход к исследованию самых разнородных по физике и конструкции систем, заложили основы теории устойчивости, установили ряд важных общих закономерностей регулирования по принципу обратной связи.
Крупный вклад в теорию регулирования внесен Н.Е. Жуковским, автором труда "О прочности движения" и первого учебника "Теория регулирования хода машин" (1909).
В первые десятилетия XX в. теория автоматического управления, вышедшая из рамок прикладной механики, формируется как общетехническая дисциплина. В этот период появляется целый ряд работ, рассматривающих приложение теории и распространяющих ее выводы на самые разнообразные технические процессы: на регулирование электрических машин и систем; двигателей внутреннего сгорания; тепловых и паросиловых устройств; турбин; различных производственных процессов. В 1932 г. появляется работа Х. Найквиста, в которой предлагается
критерий устойчивости радиотехнических усилителей с обратной связью.
Исключительно интенсивным и многогранным было развитие теории автоматического управления в послевоенный период. Это обусловлено в первую очередь развитием военной и космической техники, бурным прогрессом вычислительной техники и электроники.
В настоящее время буквально все окружающие нас технические устройства содержат в своем составе то или иное число автоматических регуляторов. Ограничиваясь для примера бытовой электроникой, перечислим лишь некоторые характерные термины: автоматическая регулировка усиления; автоподстройка частоты; стабилизация напряжения и т.д.
Системы автоматического управления (САУ) различной физической природы и совершенно различного функционального назначения могут иметь одинаковое математическое описание, то есть описываться одинаковыми уравнениями (отличаться будут лишь размерности величин). Но в САУ с одинаковым математическим описанием и процессы при управлении будут протекать одинаково, хотя действовать в них будут различные физические величины. Какие процессы могут происходить при управлении?
Во-первых, в результате приложения конечного по величине воздействия САУ должна перейти из одного равновесного состояния в другое (в противном случае она будет неустойчивой).
Во-вторых, переход из одного состояния в новое осуществляется за некоторое определенное время, на протяжении которого величина (или величины), характеризующая состояние САУ, изменяется по какому-либо закону.
В-третьих, переход САУ в новое равновесное состояние осуществляется с какой-либо точностью.
Эти вопросы, а также влияние на процесс управления отдельных параметров САУ и изучаются в настоящей дисциплине.
Причем необходимо отметить, что составление математического описания отдельных элементов или систем в целом может быть произведено лишь на основе четкого понимания физических процессов, протекающих в этих объектах и алгоритмах их функционирования. Поэтому задача получения исходного математического описания относится к предмету специальных дисциплин, в которых эти элементы изучаются.
В теории автоматического управления указанные выше вопросы изучения САУ решаются с помощью специальных методов с использованием математического описания. Отсюда следует, что возможность успешного освоения настоящей дисциплины основывается, в первую очередь, на знании высшей математики и, с учетом профиля специальности "Промышленная электроника", основ теории цепей.
 |
Классификация САУ |
|
Для ознакомления с основными видами САУ и соответствующей терминологией рассмотрим классификацию систем по ряду существенных с позиции теории автоматического управления признаков.
а). Системы разомкнутые, замкнутые и комбинированные.
В общем виде САУ с одной выходной координатой, одним задающим и одним возмущающим воздействиями представлена на рис.1.1, на котором обозначено:
О - объект управления;
УУ - управляющее устройство (регулятор);
Х - выходная величина, характеризующая состояние объекта;
Y - регулирующее воздействие;
G - задающее воздействие;
F - возмущающее воздействие.
Рис.1.1
На вход УУ помимо задающего воздействия поступает информация о возмущающем воздействии и о текущем реальном значении выходной величины. В соответствии с этим УУ полученную информацию преобразует и формирует регулирующее воздействие.
В частных случаях САУ могут иметь не все представленные связи.
В разомкнутых САУ выходная величина объекта не измеряется, то есть нет контроля за состоянием объекта. Разомкнутыми они называются потому. что в них отсутствует связь между выходом объекта и входом управляющего устройства.
Возможны варианты, в которых УУ измеряет только задающее воздействие G, либо задающее и возмущающее воздействие F. В первом варианте принято говорить, что управление осуществляется по задающему воздействию, во втором - по возмущающему.
При реализации управления по задающему воздействию команды G путем изменения Y приводят к соответствующим изменениям выходной величины Х. Точность соответствия Х и G определяется стабильностью параметров УУ и О, а также величиной возмущения.
В САУ с управлением по возмущающему воздействию (такие САУ называют еще системами, реализующими принцип управления по возмущению) регулирующее воздействие Y формируется таким, чтобы скомпенсировать отклонение выходной величины Х, вызванное измеряемым возмущением F. Для повышения точности необходимо учитывать все возможные возмущения. Практически большинство возмущений трудно измерить и преобразовать в нужный тип сигнала. Кроме того, измерение нескольких возмущений усложняет схему САУ.
В замкнутых САУ на вход УУ подаются задающее воздействие G и выходная величина объекта Х. Исходя из величины G управляющее устройство определяет соответствующее требуемое значение Х0 и, имея информацию о текущем значении Х, обеспечивает необходимое соответствие между Х и G путем воздействия на объект.
В такой САУ управляющее устройство стремится ликвидировать все отклонения Х от предписанного Х0 независимо от причин, вызывающих эти отклонения, включая любые возмущения и внутренние помехи.
САУ такого типа представляют собой замкнутый контур, образованный О и УУ. Управляющее устройство создает обратную связь вокруг объекта, связывая его выход со входом. Замкнутые САУ называют поэтому еще системами с обратной связью или системами, реализующими принцип управления по отклонению. Именно системы с обратной связью представляют основной тип САУ.
При использовании в одной системе принципов управления по отклонению и по возмущению получают комбинированную САУ. В этом случае повышается качество управления, так как увеличивается информация о состоянии объекта и внешней среды.
Проиллюстрируем (на качественном уровне, без количественной оценки) преимущества замкнутой САУ над разомкнутой по задающему воздействию на примере генератора постоянного тока, управляемого по цепи возбуждения. Схема разомкнутой системы приведена на рис.1.2.
Рис.1.2
Предположим, что обеспечено вращение вала генератора Г с неизменной угловой скоростью ω, генератор работает на линейном участке кривой намагничивания, функциональный усилитель У обеспечивает линейную зависимость тока возбуждения Iв от задающего напряжения Uз.
Управлять выходной величиной - напряжением Uн, прикладываемым к сопротивлению нагрузки Rн , можно, изменяя величину Uз путем передвижения движка потенциометра R1.
В качестве возмущающего воздействия рассмотрим изменение величины нагрузки, т.е. тока Iн.
По второму закону Кирхгофа Uн=E-Iнrвн,
где Е - э.д.с. генератора,
rвн- внутреннее сопротивление генератора.
Если ток нагрузки изменяется от 0 до какого-то максимального значения INmax, то изменение выходного напряжения ΔUN при этом составит величину (при условии, что Uз=const)
Если мощность генератора соответствует мощности нагрузки, то rвн относительно Rн составляет величину, которой нельзя пренебречь, в результате ΔUN относительно Е является величиной существенной, т.е. изменение нагрузки при неизменном задающем воздействии значительно влияет на выходное напряжение.
Далее замкнем обратную связь, т.е. подадим часть выходного напряжения, снимаемого с резистора R3 делителя напряжения на резисторах R2 и R3 и обозначенного Uос, на вход усилителя У, как показано на рис.1.3. Причем полярность напряжений должна быть такой, как показано на рис.1.3 без скобок.
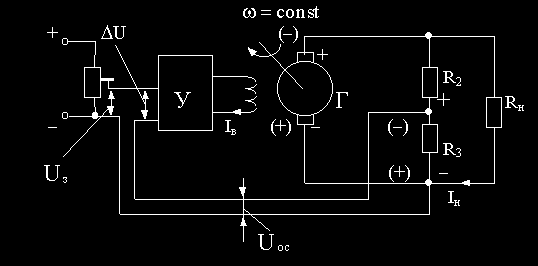
Рис.1.3
Пусть эта схема находилась в каком-то исходном установившемся состоянии, при котором 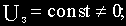 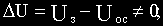 Rн=const; Iн=const; Uн=const. Rн=const; Iн=const; Uн=const.
Далее предположим, что в схеме произошло возмущение - скачком увеличилось сопротивление нагрузки и, следовательно, уменьшился ток Iн. Как схема отреагирует на это возмущение?
Вначале напряжение Uн увеличится, так как уменьшится падение напряжения на внутреннем сопротивлении генератора. Следовательно, увеличится Uос, уменьшится ΔUN (Uз осталось неизменным), пропорционально уменьшится Iв, уменьшится Е, уменьшится и выходное напряжение Uн. Указанные процессы будут происходить не мгновенно, а за какое-то конечное время, по истечении которого выходное напряжение с
какой-то точностью вернется к исходному значению. Если бы произошло не уменьшение, а увеличение тока нагрузки, то все величины изменялись бы в противоположную сторону.
В рассмотренной схеме изменение тока нагрузки (возмущающего воздействия) уже не приводит к значительному изменению выходного напряжения.
Но рассмотрим еще один аспект: как бы работала схема. если бы генератор подключили с противоположной полярностью (указана на рис.1.3 в скобках).
При увеличенииRн и уменьшении Iн вначале Uн увеличится, как и в предыдущем случае. Увеличится и Uос, но теперь 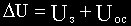 , таким образом увеличится , таким образом увеличится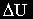 , увеличатся Iв и Е, следовательно еще больше увеличится Uн. Таким образом, вызванное на начальном этапе после возмущения увеличение Uн приводит к увеличению , увеличатся Iв и Е, следовательно еще больше увеличится Uн. Таким образом, вызванное на начальном этапе после возмущения увеличение Uн приводит к увеличению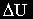 , которое в свою очередь увеличивает Uн и т.д. Схема стала неработоспособной (в первом случае обратная связь была отрицательной, во втором - положительной). , которое в свою очередь увеличивает Uн и т.д. Схема стала неработоспособной (в первом случае обратная связь была отрицательной, во втором - положительной).
Одна из задач теории автоматического управления (ТАУ) - дать точную количественную оценку всем рассмотренным в настоящем примере явлениям.
б). Системы линейные и нелинейные. Линейной называется система, которая описывается только линейными уравнениями. Чтобы система была нелинейной, достаточно иметь в ее составе хотя бы одно нелинейное звено.
Для линейных САУ применим принцип суперпозиции: реакция системы на любую комбинацию внешних воздействий равна сумме реакций на каждое из этих воздействий, поданных на систему порознь.
Необходимо отметить, что реальные линейные системы являются таковыми лишь в определенном диапазоне изменения воздействий. Если не ограничивать диапазон изменения воздействий, то любая САУ становится нелинейной.
в). Системы непрерывного и дискретного действия. Непрерывная система состоит из звеньев, выходная величина которых изменяется плавно (без скачков) при плавном изменении входного воздействия. Дискретная САУ должна содержать хотя бы одно звено дискретного действия. Под звеном дискретного действия понимается звено, у которого выходная величина изменяется скачками при плавном изменении входной.
г). Системы стационарные и нестационарные.
Стационарной называется система, все параметры которой не изменяются во времени. Нестационарная система - это система с переменными во времени параметрами. При математическом описании такой системы некоторые коэффициенты являются функциями времени.
В качестве примера нестационарной системы можно привести самолет. В полете по мере расхода горючего масса самолета уменьшается.
д). Одномерные и многомерные САУ.
Разделение на данном уровне классификации производится по числу выходных координат объекта управления.
Пример одномерной системы - источник питания постоянного тока (выходная координата одна - среднее значение напряжения), двухмерной - источник питания переменного тока (выходных координат две - частота и эффективное значение напряжения), трехмерной - радиолокационная станция слежения за летательными аппаратами (выходных координат три - дальность, угол места, азимут).
е). Системы стабилизации, программного управления и следящие.
Системы стабилизации характеризуются неизменностью задающего воздействия. Задача таких систем - поддержание с допустимой ошибкой выходной величины при наличии возмущающих воздействий.
Системы программного управления отличаются тем, что задающее воздействие изменяется по заранее установленному закону.
В следящих системах задающее воздействие также является величиной переменной, но заранее закон его изменения неизвестен. Источником сигнала является внешнее явление.
Таким образом, для систем стабилизации G=const, для следящих систем и систем программного управления G=var.
ж). Системы оптимальные и неоптимальные (обыкновенные).
В оптимальных системах должно обеспечиваться оптимальное значение какого-либо из параметров функционирования. Но так как связь между отдельными параметрами обычно противоречивая, то на остальные параметры накладывается ограничение (значение их должно быть не хуже заданного уровня). В обыкновенных системах указанная задача оптимизации не ставится.
В завершение вводного раздела введем понятие функциональной схемы (не путать со схемой электрической функциональной !), принятое в теории автоматического управления. При составлении функциональной схемы система разбивается на такие узлы, каждый из которых несет законченное функциональное назначение (сложность каждого из таких узлов при этом значения не играет). Выделенные таким образом узлы на функциональной схеме соединяются линиями связи с указанием направления распространения сигналов.
Какими бы ни были системы автоматического управления (хотя бы в соответствии с представленной здесь классификацией, физическим принципом действия, областью применения и т.д.), они в целом имеют одну и ту же функциональную схему, но только некоторые элементы могут отсутствовать или, наоборот, повторяться. Такая обобщенная функциональная схема представлена на рис.1.4.
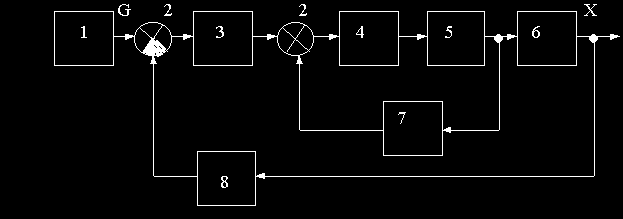
Рис.1.4
Здесь обозначено: 1- задающее устройство, формирующее задающее воздействие G; 2 - сумматор (сектор круга зачерняется, если подходящий к нему сигнал имеет знак "минус", например, реализуется отрицательная обратная связь); 3 - последовательное корректирующее устройство; 4 - усилитель; 5 - исполнительный элемент; 6 - объект управления; 7 - местная обратная связь (параллельное корректирующее устройство); 8 - главная обратная связь.
|